4 Vitesse d’une réaction enzymatique
Dans cette partie, nous allons revenir sur le modèle de Michaelis-Menten (§ 3.3) proposé en 1913 par l’allemand Leonor Michaelis et la canadienne Maud Menten pour décrire la vitesse (\(v\)) d’une réaction chimique catalysée par une enzyme agissant sur un substrat (\([S]\)) unique pour donner un produit (Michaelis et Menten, 1913) : \[ v([S]) = \frac{v_{max} [S]}{K_M + [S]} \] On parle de cinétique enzymatique. Il s’agit d’une relation monotone croissante sans point d’inflexion, telle que \(\lim\limits_{[S] \to + \infty } v\left( {[S]} \right) = {v_{\max }}\) et \(v(K_M) = \frac{v_{max}}{2}\).
Dans cette relation, \([S]\) est la variable indépendante explicative (on l’appelle aussi variable de contrôle), tandis que \(v\) est la variable dépendante à expliquer.
4.1 Les observations
Nous allons travailler avec des données tirées de la littérature scientifique (Fig. 11).
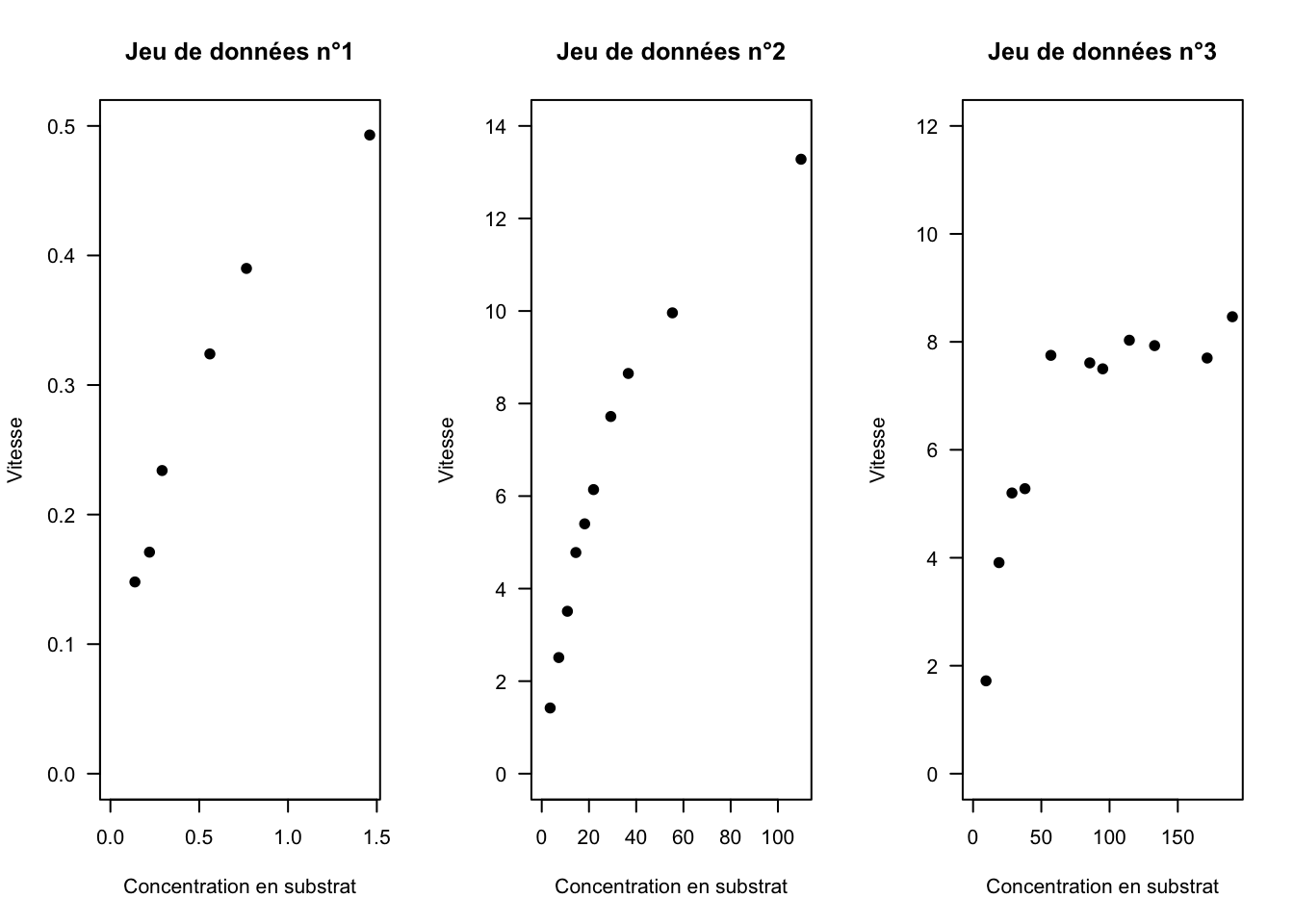
Fig. 11: Représentation graphique de la relation vitesse versus concentration en susbtrat pour trois jeux de données tirés de la littérature (Ritchie et Prvan, 1996).
La tendance moyenne des données semble suivre le modèle de Michaelis-Menten avec, pour chaque jeu de données, des valeurs des paramètres \(v_{max}\) et \(K_M\) différentes.
Télécharger le jeu de données n°1
4.2 La méthode de régression
4.2.1 Généralités
Soit \((x_{i}, y_{i})\) les couples de valeurs observées pour \([S]\) et \(v\) dans un jeu de données, avec \(i=1,...,n\) et \(n\) le nombre d’observations dans le jeu de données.
Si on suppose que la concentration en substrat peut être déterminée avec suffisamment de précision, alors on peut considérer que les \(x_{i}\) sont connus “sans erreur.” Par contre, il est souvent difficile expérimentalement de mesurer la vitesse d’une réaction chimique, ce qui nous conduit à considérer que les \(y_{i}\) seront distribuées aléatoirement et selon une certaine loi autour de la tendance moyenne décrite par le modèle de Michaelis-Menten. La variable \(v\) étant une variable quantitative continue, il est raisonnable de supposer qu’elle se distribue selon une loi de probabilité gaussienne, c’est-à-dire une loi normale (ou loi de Gauss). Ainsi : \[ y_{i} \sim \mathcal{N}(v(x_{i}), \sigma) \Leftrightarrow y_{i} = v(x_{i}) + \varepsilon_{i} \] avec \(\varepsilon_{i} \sim \mathcal{N}(0, \sigma)\). On appelle les \(\varepsilon_{i}\) les résidus, c’est-à-dire les écarts entre les valeurs observées et les valeurs théoriques moyennes prédites par la partie déterministe du modèle.
Il s’agit d’un modèle statistique dans lequel la fonction \(v(x_{i})\) correspond à la partie déterministe et la loi normale à la partie stochastique. C’est un modèle qui compte trois paramètres, \(v_{max}\), \(K_M\) et \(\sigma\), dont nous allons chercher à estimer les valeurs pour chacun des jeux de données ci-dessus. Ainsi, nous allons chercher à optimiser la valeur des paramètres pour que la courbe représentant la tendance moyenne passe “au mieux” entre les points ; nous allons faire ce que l’on appelle de la régression.
Le terme “régression” a été introduit par Francis Galton à la suite d’une étude sur la taille des descendants de personnes de grande taille, qui diminue de générations en générations vers une taille moyenne, c’est-à-dire que leur taille régresse (Galton, 1890).
4.2.2 Le critère des moindres carrés
Lorsque l’on a affaire à un modèle statistique gaussien, l’optimation des paramètres consiste à minimiser la Somme des Carrés des Écarts (\(SCE\)) entre les observations et la valeur moyenne prédite par le modèle, c’est-à-dire à minimiser la fonction suivante :
\[SCE\left( \Theta \right) = \sum\limits_{i = 1}^{{n}} {{{\left( {{y_{i}} - v\left( {{x_{i}}} \right)} \right)}^2}} \]
avec \(\Theta = \left( v_{max}, K_M \right)\) le vecteur des paramètres à estimer dans le cas du modèle de Michaelis-Menten.
On parle d’estimation selon le critère des moindres carrés.
Pour être exhaustif, il y a un troisième paramètre à estimer, \(\sigma\), lié à la distribution normale supposée des observations autour de v\((x_i)\). Celui-ci est estimé une fois le processus de minimisation terminé par : \[\hat \sigma = \sqrt {\frac{{SC{E_{\min }}}}{{n - 2}}} \]
Graphiquement, minimiser la \(SCE\) revient à minimiser la somme des distances représentées par les segments noirs sur la figure ci-dessous (Fig. 12).
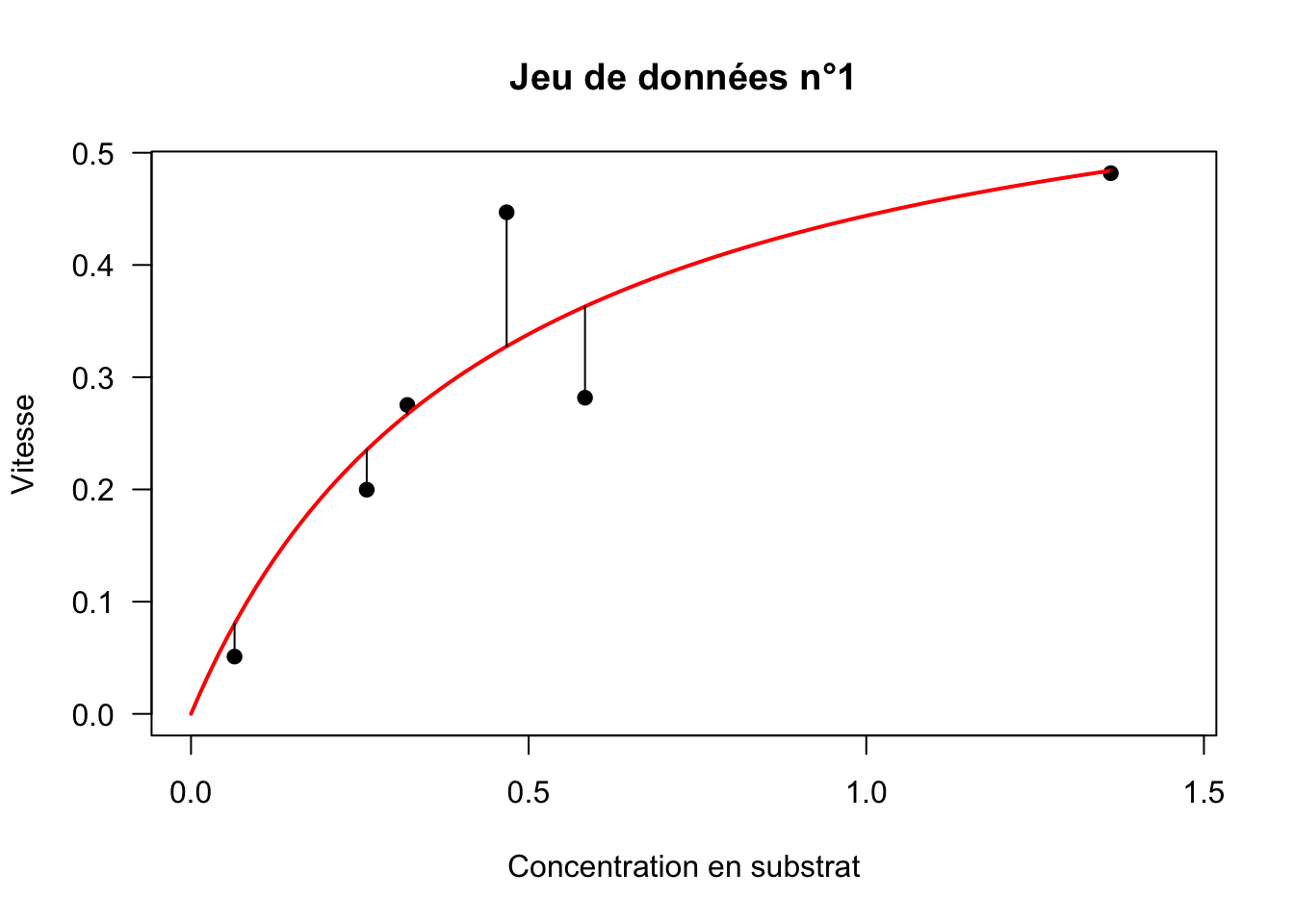
Fig. 12 : Régression du modèle de Michaelis-Menten sur le jeu de données numéro 1.
Dans le cas du modèle de Michaelis-Menten :
la partie déterministe est non linéaire, c’est-à-dire que les dérivées partielles de \(v([S])\) par rapport aux deux paramètres \(v_{max}\) et \(K_M\) dépendent encore des paramètres ;
la partie stochastique est gaussienne.
On parle donc de régression non linéaire gaussienne et c’est ce qui nous occupera pour cette troisième partie. Néanmoins, il existe d’autres formes de régression : la régression linéaire gaussienne, la régression linéaire non gaussienne (par exemple, la régression logistique), la régression non linéaire non gaussienne (par exemple, un modèle concentration-effet pour des données de survie binaires).
4.2.3 Algorithmes de minimisation
La plupart du temps, en régression non linéaire gaussienne, la minimisation de la \(SCE\) n’admet pas de solution analytique, c’est-à-dire pas de solution exacte. Cette minimisation se fait donc par résolution numérique selon une méthode itérative qui impose :
une évaluation initiale “à l’oeil” des paramètres ;
des calculs itératifs pour converger vers le vecteur des paramètres qui minimise la SCE.
Parmi les algorithmes de minimisation les plus connus, on trouve : l’algorithme de Gauss-Newton, l’algorithme de Golub-Pereyra ou encore l’algorithme de Levenberg-Marquardt. Ces algorithmes reposent tous sur des déplacements à petits pas dans la direction de plus grande pente de la fonction SCE, en linéarisant le modèle à chaque itération ; ils sont pour la plupart implémentés dans la fonction nls du logiciel R.
A l’époque de Michaelis-Menten, et pendant de nombreuses années ensuite, l’utilisation de ces algorithmes n’était pas permise, soit parce que les méthodes n’avaient pas encore été découvertes, soit parce qu’elles nécessitaient de gros moyens de calculs. Il a donc fallu ruser ; en particulier, plusieurs méthodes ont été proposées pour transformer les données de cinétique enzymatique de façon à produire une relation linéaire et ainsi faciliter l’estimation des paramètres (Atkins et Nimmo, 1975).
4.3 Transformations linéaires
S’il existe près d’une dizaine de transformations linéaires, nous ne verrons que les trois transformations les plus couramment utilisées (Ritchie et Prvan, 1996) . La rédaction de ce paragraphe est très largement inspirée de la fiche tdr47 élaborée par J.R. Lobry.
4.3.1 La transformation de Lineweaver & Burk
La transformation linéaire de Lineweaver & Burk (1934) consiste à représenter \(y = 1/v\) en fonction de \(x = 1/[S]\) (Fig. 13) :
\[\frac{1}{v} = \frac{K_M}{v_{max}}\frac{1}{[S]} + \frac{1}{v_{max}}\]
Il s’agit bien d’une équation de droite dont la pente est donnée par \(\frac{K_M}{v_{max}}\) et l’ordonnée à l’origine par \(1/v_{max}\). A cela s’ajoute le paramètre \(\sigma\) de la loi normale.
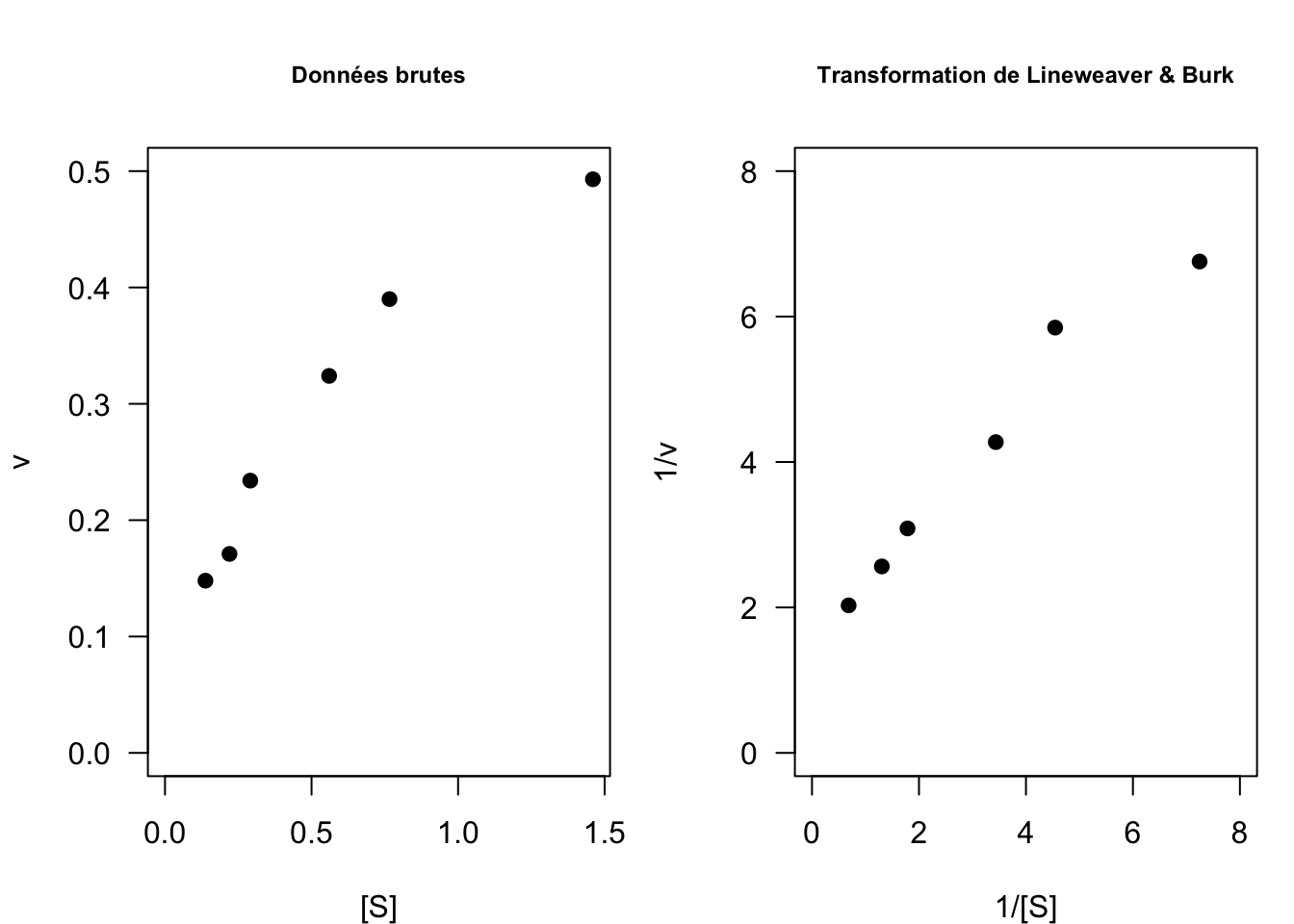
Fig. 13 : Comparaison des données brutes et transformées selon Lineweaver & Burk sur le jeu de données n°1.
4.3.2 La transformation de Eadie et Hofstee
La transformation linéaire de Eadie et Hofstee (Eadie 1942, Hofstee 1952) consiste à représenter \(y = v\) en fonction de \(x = v/[S]\) (Fig. 14) :
\[ v([S]) = - K_M\frac{v}{[S]} + v_{max}\]
Il s’agit bien d’une équation de droite dont la pente est donnée par \(-K_M\) (\(<0\)) et l’ordonnée à l’origine par \(v_{max}\). A cela s’ajoute le paramètre \(\sigma\) de la loi normale.
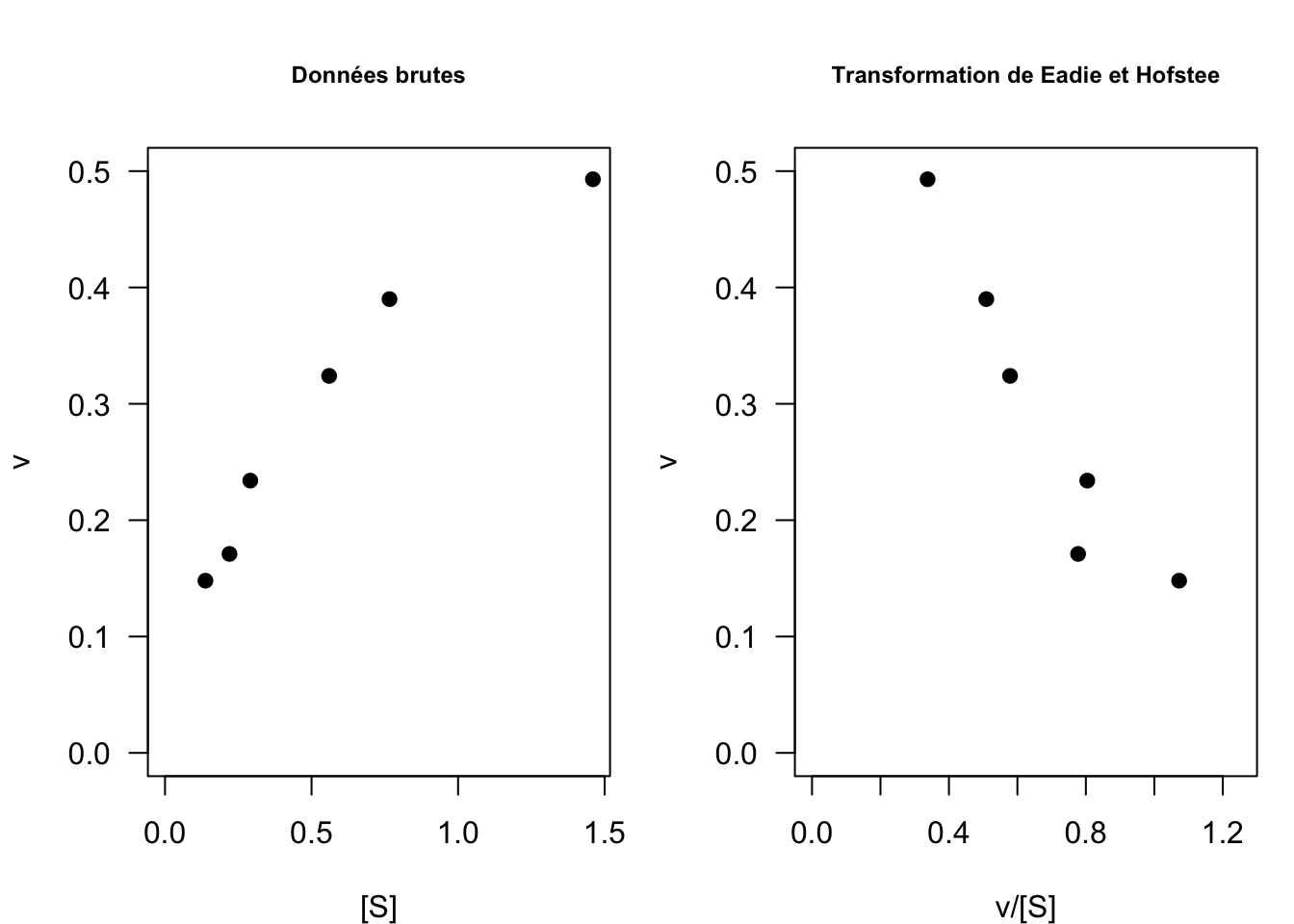
Fig. 14 : Comparaison des données brutes et transformées selon Eadie et Hofstee sur le jeu de données n°1.
4.3.3 La transformation de Wilkinson
La transformation linéaire de Wilkinson (1961) consiste à représenter \(y = [S]/v\) en fonction de \(x = [S]\) (Fig. 15) :
\[\frac{[S]}{v} = \frac{1}{v_{max}}[S] + \frac{K_M}{v_{max}}\]
Il s’agit bien d’une équation de droite dont la pente est donnée par \(1/v_{max}\) et l’ordonnée à l’origine par \(K_M/v_{max}\). A cela s’ajoute le paramètre \(\sigma\) de la loi normale.
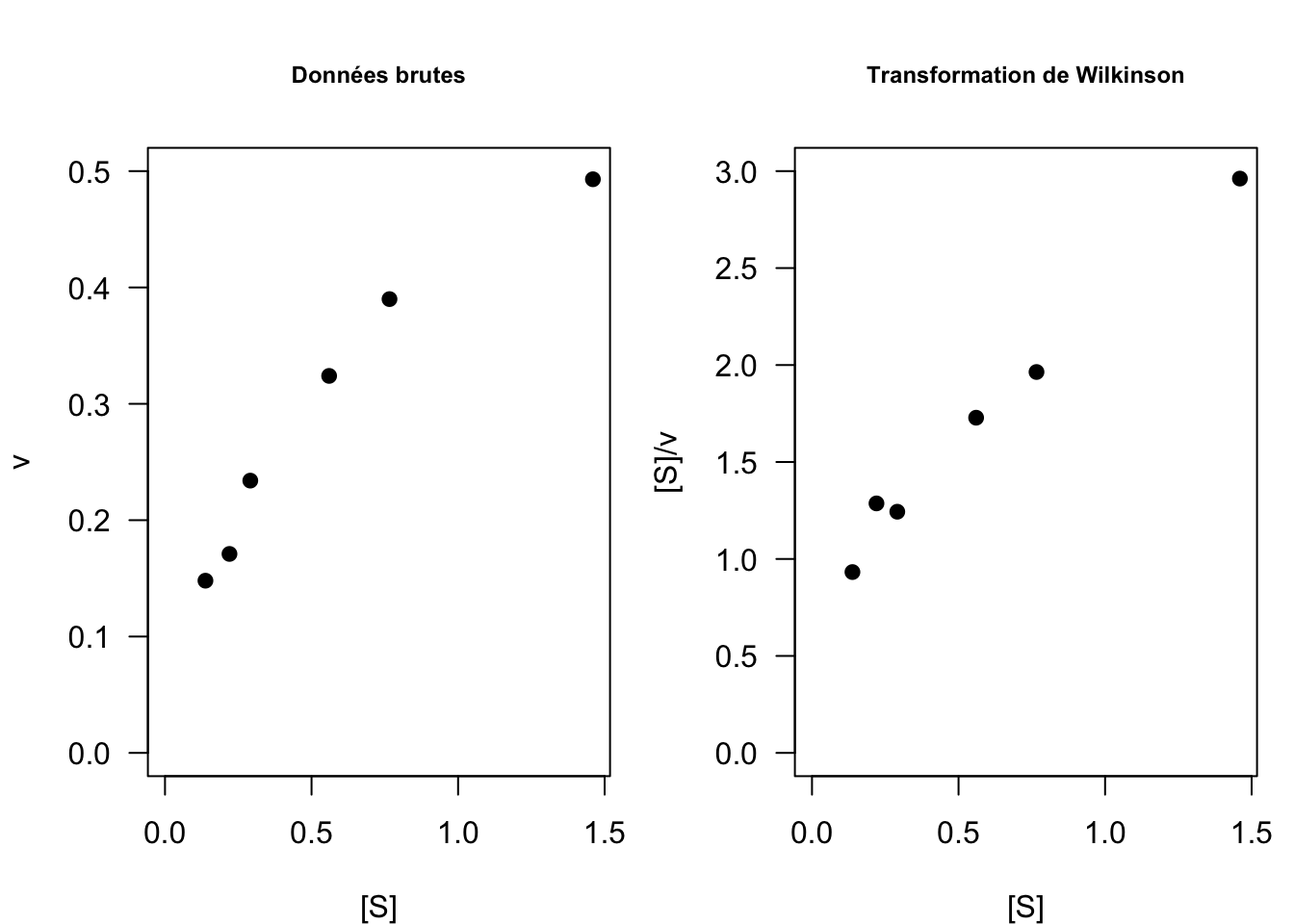
Fig. 15 : Comparaison des données brutes et transformées selon Wilkinson sur le jeu de données n°1.
4.4 Retour à la régression gaussienne
Lorsque l’on fait de la régression, on cherche donc à estimer les paramètres d’un modèle à partir de données expérimentales ; on dit qu’on cherche à ajuster un modèle à des données. Nous allons maintenant voir comment procéder grâce au logiciel R (pour plus de détails, voir ici). Nous utiliserons le jeu de données numéro 1 pour illustrer les différents points.
4.4.1 Ajuster un modèle linéaire gaussien avec R
Nous travaillerons avec la transformation linéaire de Lineweaver & Burk dont la partie déterministe s’écrit : \[y = \frac{K_M}{v_{max}} x + \frac{1}{v_{max}}\] avec \(x = 1/[S]\) et \(y = 1/v\).
1. On commence par importer les données sous la forme d’un tableau à deux colonnes : S pour la concentration substrat (notre variable explicative) et V pour la vitesse de la réaction enzymatique (notre variable à expliquer).
# Création du tableau de données
dataMM1 <- read.table("dataMM1.txt", header = TRUE)
# ATTENTION au chemin d'accès à votre propre fichier "dataMM1.txt"# Visualisez le jeu de données
par(mar = c(4, 4, 0.2, 0.2)) # réglage des marges
plot(dataMM1, las = 1, pch = 19)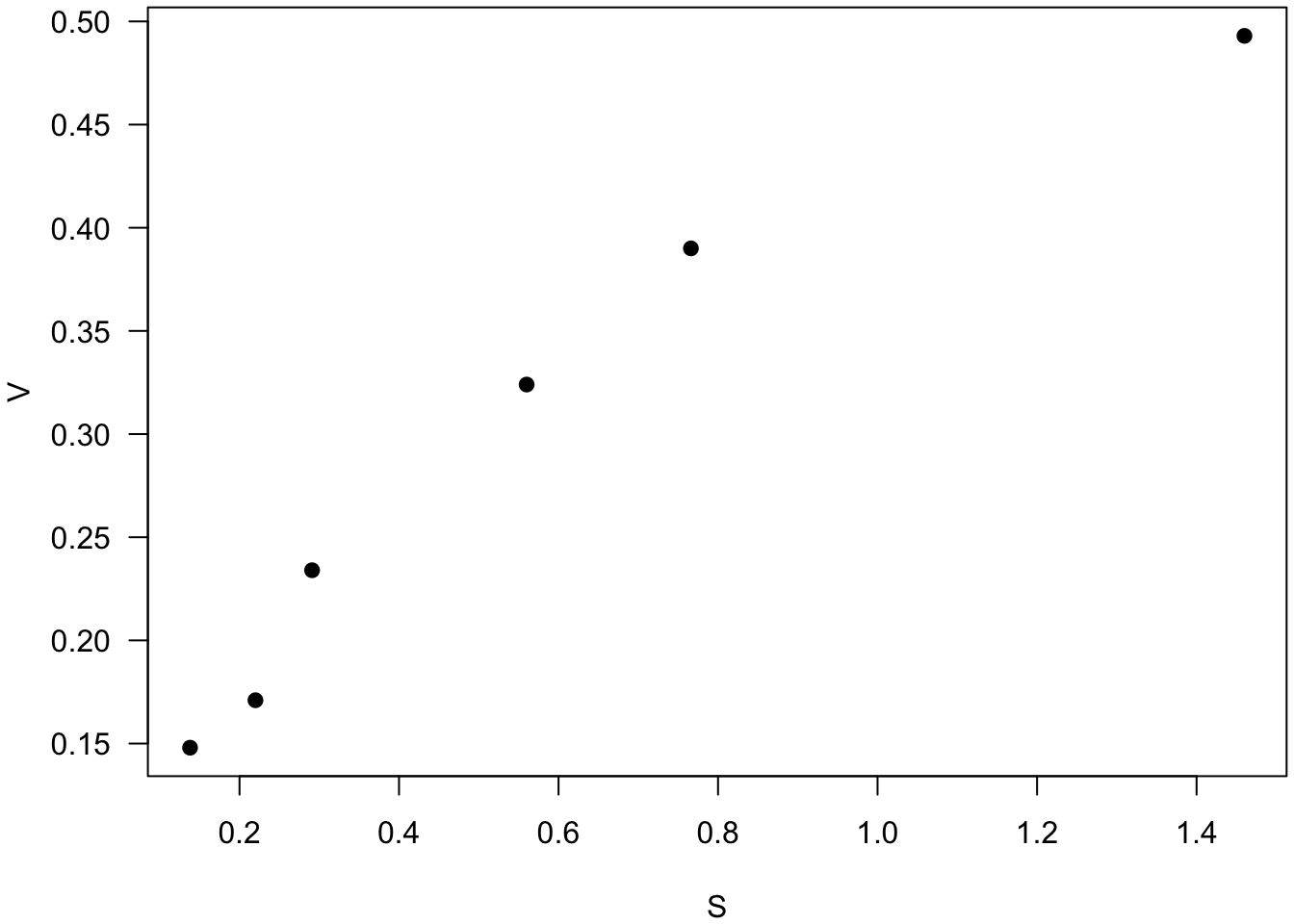
n <- nrow(dataMM1) # Nombres d'observations dans le jeu de données
# Transformez les données selon Lineweaver \& Burk
x <- 1/dataMM1$S
y <- 1/dataMM1$V2. On ajuste le modèle linéaire de Lineweaver & Burk à l’aide de la fonction lm (pour “linear model”).
m <- lm(y ~ x)
# On demande les résultats de l'ajustement
summary(m)
Call:
lm(formula = y ~ x)
Residuals:
1 2 3 4 5 6
-0.40673 0.71770 -0.02187 0.03369 -0.12712 -0.19567
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.70846 0.30327 5.634 0.00489 **
x 0.75279 0.07815 9.632 0.00065 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4291 on 4 degrees of freedom
Multiple R-squared: 0.9587, Adjusted R-squared: 0.9483
F-statistic: 92.78 on 1 and 4 DF, p-value: 0.0006497On obtient en sortie les valeurs des résidus (Residuals), c’est-à-dire les écarts entre observations et valeurs calculées par le modèle, les estimations moyennes (Estimate) des deux paramètres \(1/v_{max}\) (Intercept) et \(K_M/v_{max}\) (x), avec leur écart-type (Std. Error). L’estimation moyenne de \(\sigma\) est donnée par la quantité Residual standard error (ici \(0.4291\)).
# Explorer l'objet 'm' à l'aide de la fonction names()
names(m) [1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model" # Vous constatez que vous avez accès à différents sous-objets.
# Par exemple les coefficients de la droite de régression
m$coefficients(Intercept) x
1.7084585 0.7527938 Précision et erreur relative
On peut se faire une idée de la précision avec laquelle un paramètre \(\alpha\) a été estimé en évaluant l’erreur relative comme suit :
\[ER(\alpha) = \frac{SE(\alpha)}{moy(\alpha)} t_{(0.975;n-p)}\]
avec \(moy(\alpha)\) la moyenne du paramètre \(\alpha\), \(SE(\alpha)\) l’écart-type (ou erreur standard, standard error en anglais) du paramètre \(\alpha\), \(p\) le nombre de paramètres dans la partie déterministe du modèle (ici \(p=2\)), \(n\) la taille du jeu de données (ici \(n=6\)) et \(t_{(0.975;n-p)}\) le quantile \(97.5\%\) de la loi de Student à \(n-p\) degrés de liberté (\(t_{(0.975;n-p)} \sim 2\)).
La précision (exprimée en \(\%\)) est jugée d’autant meilleure que \(ER\) est petite.
estim <- summary(m)$coefficients[,"Estimate"] # estimations moyennes
SE <- summary(m)$coefficients[,"Std. Error"] # écart-types
ER <- 100*qt(0.975, n-2)*SE/estim # erreurs relatives
ER # affichage (en %)(Intercept) x
49.28430 28.82484 - Qu’en pensez-vous ?
3. On représente ensuite les données sur lesquelles on peut superposer la droite ajustée, fonction abline, et éventuellement aussi les résidus que l’on récupère dans l’objet fitted(m).
par(mfrow=c(1,1)) # pour n'avoir qu'un seul graphe dans la fenêtre graphique
par(mar=c(4, 4, 0.2, 0.2)) # réglage des marges
plot(x, y, pch = 19)
abline(m) # superposition de la droite de régression
segments(x, y, x, fitted(m)) # ajout des distances entre observations et valeurs théoriques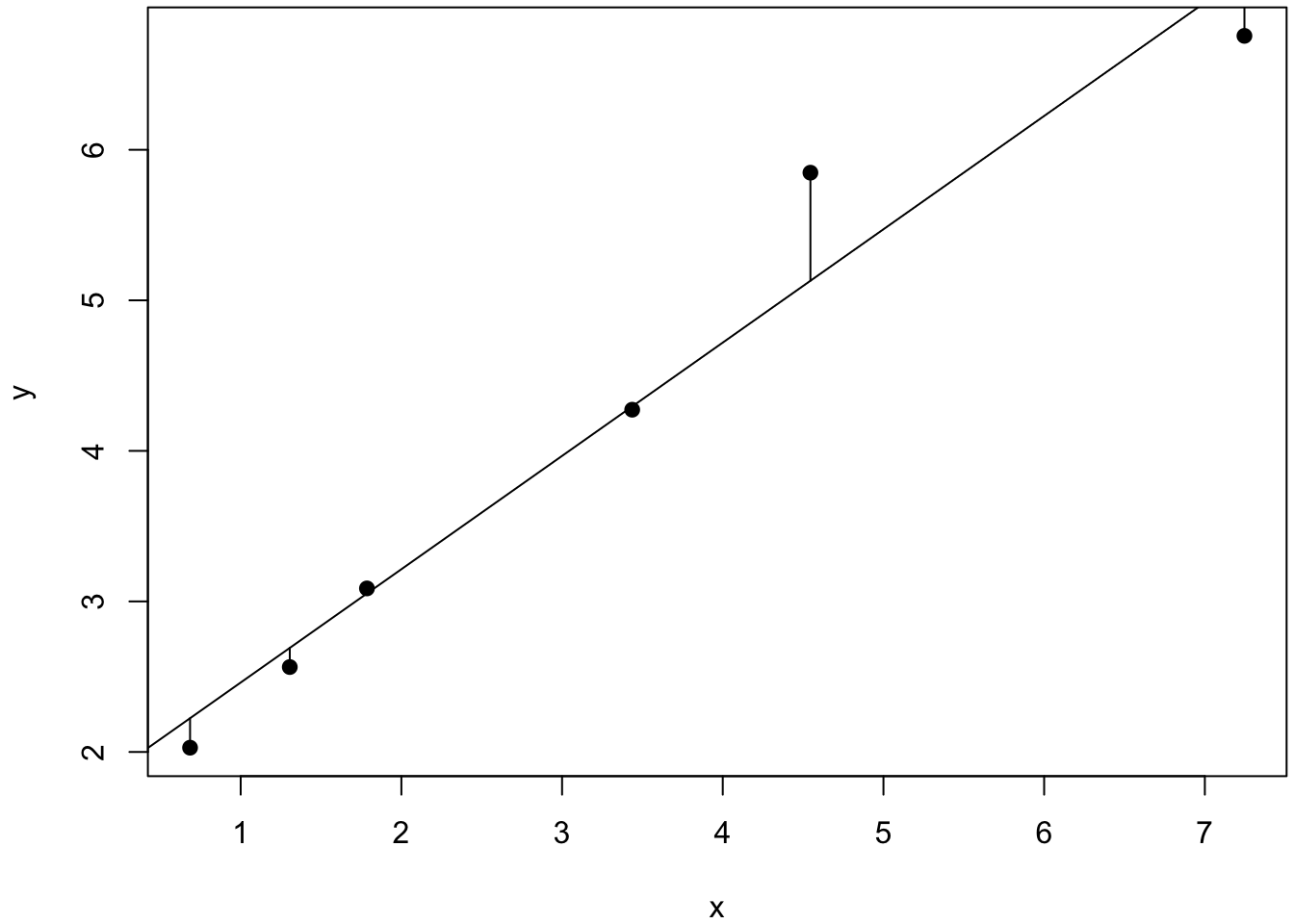
- Améliorez l’esthétique du graphe si le coeur vous en dit.
On fait ensuite l’analyse des résidus.
En effet, notre modèle statistique complet s’écrit :
\[ Y_{obs} = y_{theo} + \varepsilon\]
avec \(\varepsilon \sim \mathcal{N}(0, \sigma)\). Autrement dit, les résidus doivent vérifier plusieurs hypothèses :
ils doivent être indépendants les uns des autres : on parle d’absence d’auto-corrélation entre les résidus ;
ils doivent suivre une loi normale ;
la variance de la loi normale des résidus est constante et égale à \(\sigma^2\) : on parle d’homoscédasticité.
4. On représente graphiquement les résidus
# Graphe des résidus en fonction des valeurs prédites
sigma <- summary(m)$sigma # écart-type résiduel
# fitted(m) fournit les valeurs théoriques
# residuals(m) fournit les résidus
plot(fitted(m), residuals(m), pch = 19,
main="Résidus en fonction des valeurs prédites",
las=1, ylim=c(-2.2*sigma,2.2*sigma))
abline(h=0, col="blue") # droite horizontale d'abcisse 0
# On trace ensuite les droites horizontales pour -2*sigma et +2*sigma
abline(h=c(-2*sigma,2*sigma), lty=2, col="blue") # pointillés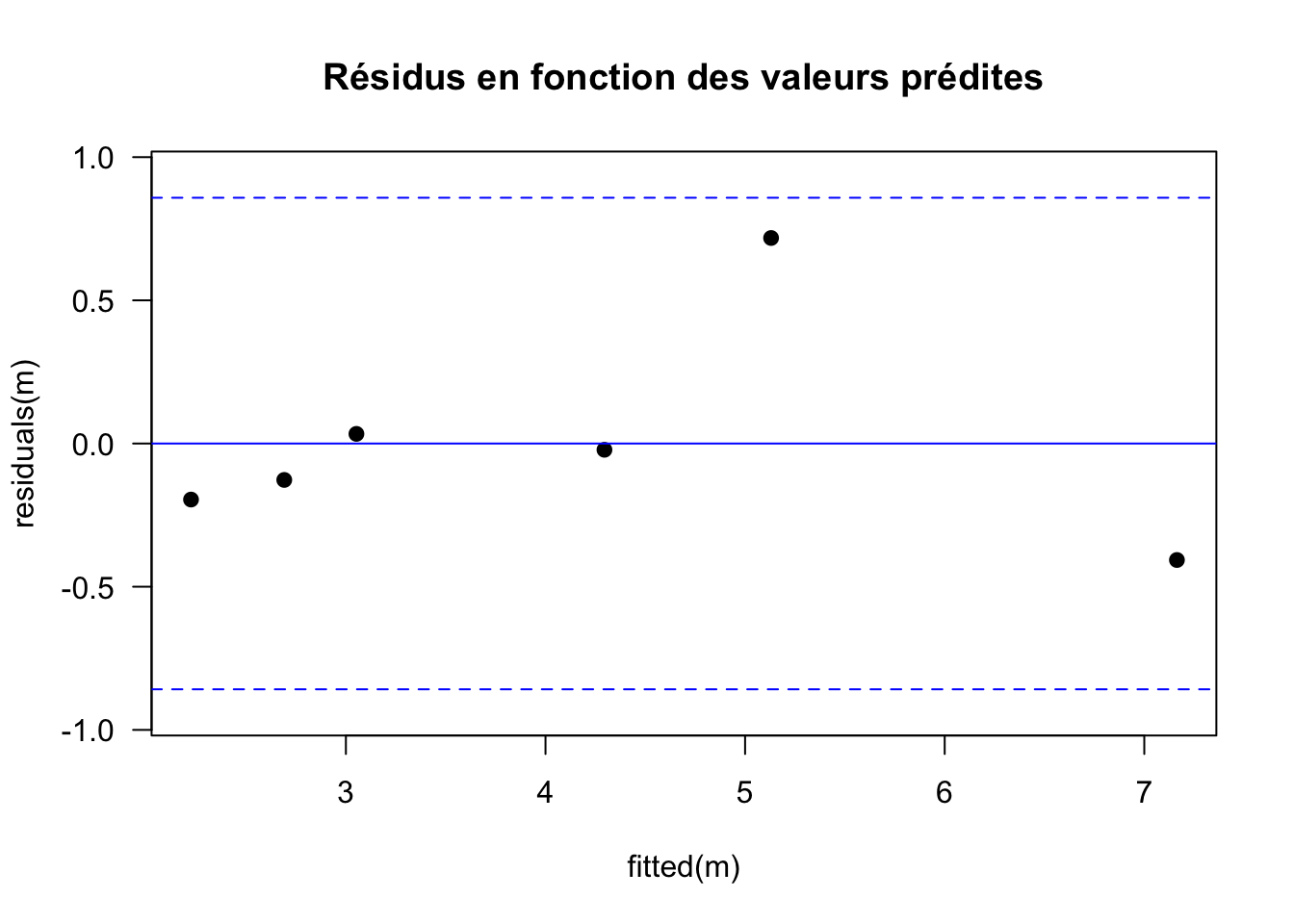
Sur ce type de graphe, on s’attend à une répartition aléatoire des résidus selon une loi normale de variance \(\sigma^2\) constante avec environ \(95\%\) des résidus dans l’intervalle \([−2 \sigma ; 2 \sigma]\), c’est-à-dire entre les deux droites horizontales en pointillés bleus.
Que faut-il repérer sur le graphe des résidus ?

Les résidus ne sont pas distribués aléatoirement \(\rightarrow\) on rejette le modèle

On voit un graphe en entonnoir (hétéroscédasticité) \(\rightarrow\) on rejette le modèle

Il y a des résidus extrêmes (outliers) \(\rightarrow\) on rejette le modèle

\(\rightarrow\) Rien ne permet de rejeter le modèle.
5. On vérifie la normalité des résidus
On peut représenter graphiquement leurs quantiles en fonction des quantiles d’une loi normale. On s’attend sur ce graphe à ce que les points s’alignent le long de droite de Henry (en trait plein ci-dessous).
# Graphe des quantiles de nos résidus (axes des x)
# en fonction des quantiles théoriques (axes des y)
# sous l'hypothèse de la loi normale N(0, sigma)
qqnorm(residuals(m), las = 1, pch = 19)
# Ajout de la droite de Henry
qqline(residuals(m))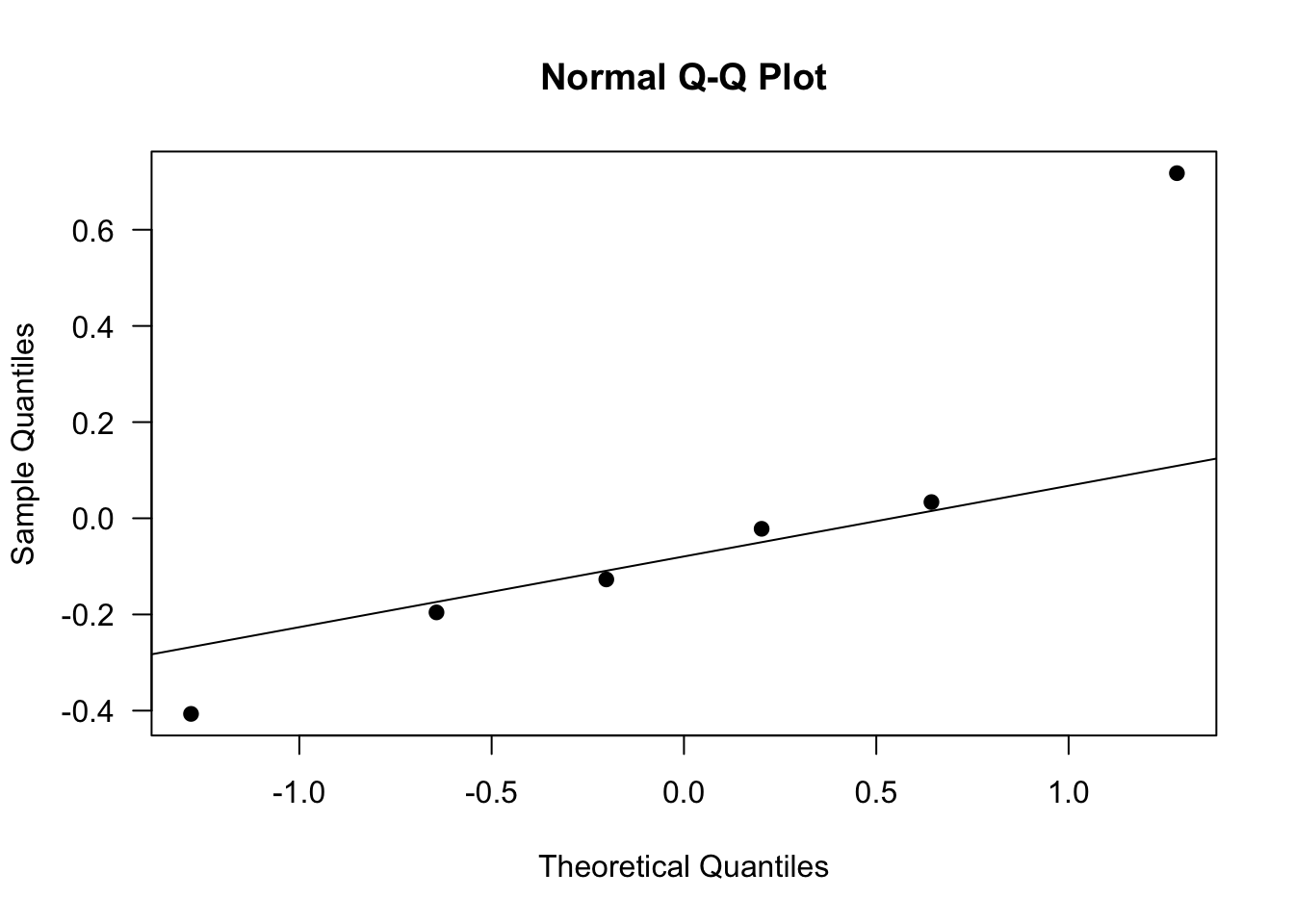
Moyennes et variances
Il faut veiller au fait qu’on travaille ici avec la transformation de Lineweaver & Burk dont les paramètres sont \(1/v_{max}\) et \(K_M/v_{max}\). Ce sont donc ces deux paramètres que l’on estime et non pas directement les paramètres \(v_{max}\) et \(K_M\) du modèle de Michaelis-Menten.
De manière générale, on retiendra les résultats suivants :
Relation entre les moyennes : \[moy\left( {\frac{1}{\alpha}} \right) = \frac{1}{moy(\alpha)}\] \[moy\left( {\frac{\alpha}{\beta}} \right) = \frac{moy(\alpha)}{moy(\beta)}\]
Une approximation de l’erreur standard (\(SE\)) sur l’inverse de \(\alpha\) est : \[SE\left( {\frac{1}{\alpha}} \right) \sim \frac{SE(\alpha)}{\alpha^2}\]
Si on néglige les termes de covariance, une approximation de l’erreur standard d’un rapport est : \[SE\left( {\frac{\alpha}{\beta}} \right) \sim \frac{\alpha}{\beta}\sqrt {{{\left( {\frac{{SE(\alpha)}}{\alpha}} \right)}^2} + {{\left( {\frac{{SE(\beta)}}{\beta}} \right)}^2}} \]
6. Retour aux paramètres de Michaelis-Menten
# Valeurs moyennes des paramètres
vmax <- 1/estim["(Intercept)"]
KM <- estim["x"]*vmax
data.frame(vmax, KM, row.names="Parameters") vmax KM
Parameters 0.585323 0.4406275# Erreurs standards
SE.vmax <- SE["(Intercept)"]/estim["(Intercept)"]^2
tmp <- sqrt((SE["(Intercept)"]/estim["(Intercept)"])^2+(SE["x"]/estim["x"])^2)
SE.KM <- (estim["x"]/estim["(Intercept)"])*tmp
data.frame(SE.vmax, SE.KM, row.names="Std.errors") SE.vmax SE.KM
Std.errors 0.1038999 0.09061058# Calcul de la précision = erreur relative
ER.vmax <- 100*qt(0.975, n-2)*SE.vmax/vmax
ER.KM <- 100*qt(0.975, n-2)*SE.KM/KM
data.frame(ER.vmax, ER.KM, row.names="ER(%)") ER.vmax ER.KM
ER(%) 49.2843 57.09478- Qu’en pensez-vous ?
Vous voilà prêts maintenant à apprendre les instructions R pour faire de la régression non linéaire.
4.4.2 Modèle non linéaire gaussien avec R
Nous allons donc maintenant revenir au modèle de Michaelis-Menten dans sa formulation initiale :
\[v([S]) = \frac{v_{max} [S]}{K_M + [S]}\]
Nous garderons le jeu de données n°1 pour illustrer les différentes instructions. Nous utiliserons la librairie nlstools du logiciel R qui met à disposition tout un panel d’outils de visualisation et d’analyse des résultats (Baty et al., 2015).
1. Prévisualisation du modèle
Comme évoqué plus haut (§ 4.2.3), les algorithmes de minimisation du critère des moindres carrés, nécessitent de donner aux paramètres des valeurs initiales. On peut faire cela “à l’oeil,” ou bien se référer à la signification biologique et/ou géométrique des paramètres (Fig. 5). On peut donc s’aider des données elles-mêmes pour trouver des valeurs initiales des paramètres (Fig. 11). Ainsi, pour le jeu de données 1, on a \(v_{max} \approx 0.5\) et \(K_M \approx 0.3\).
Vérifions avec R qu’on n’est pas loin des valeurs optimales.
library(nlstools)# ATTENTION : choisir le chemin d'accès vers votre propre fichier
dataMM1 <- read.table("dataMM1.txt", header=TRUE)n <- nrow(dataMM1) # nombre d'observations
# Implémentation du modèle
# ATTENTION : le nom des variables doit correspondre exactement
# aux en-têtes de colonne du jeu de données. Ici S et V.
modeleMM <- as.formula("V ~ vmax * S/(KM + S)")
# valeurs initiales des paramètres
valinit <- list(vmax = 0.5, KM = 0.3)
par(mfrow = c(1, 1))
par(mar = c(4, 4, 0.2, 0.2))
preview(formula = modeleMM, data = dataMM1, start = valinit)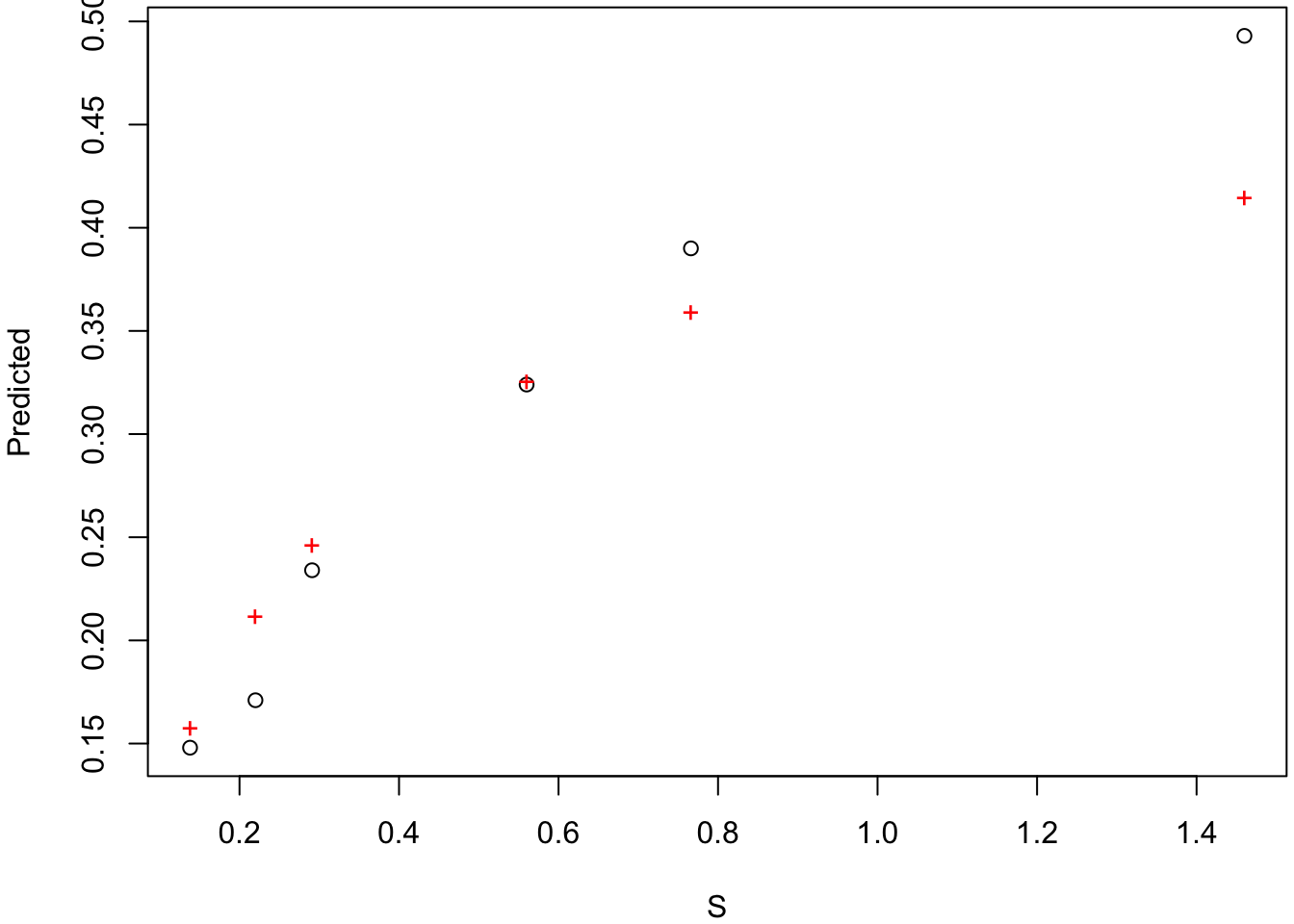
La valeur RSS: 0.00895 fournie par la fonction preview() après le graphe correspond à la valeur de la \(SCE\) pour les valeurs initiales choisies (valinit).
2. Ajustement par régression non linéaire
ajusMM <- nls(formula = modeleMM, data = dataMM1, start = valinit)
# Pour visualiser le graphe de l'ajustement :
plotfit(ajusMM, smooth = TRUE)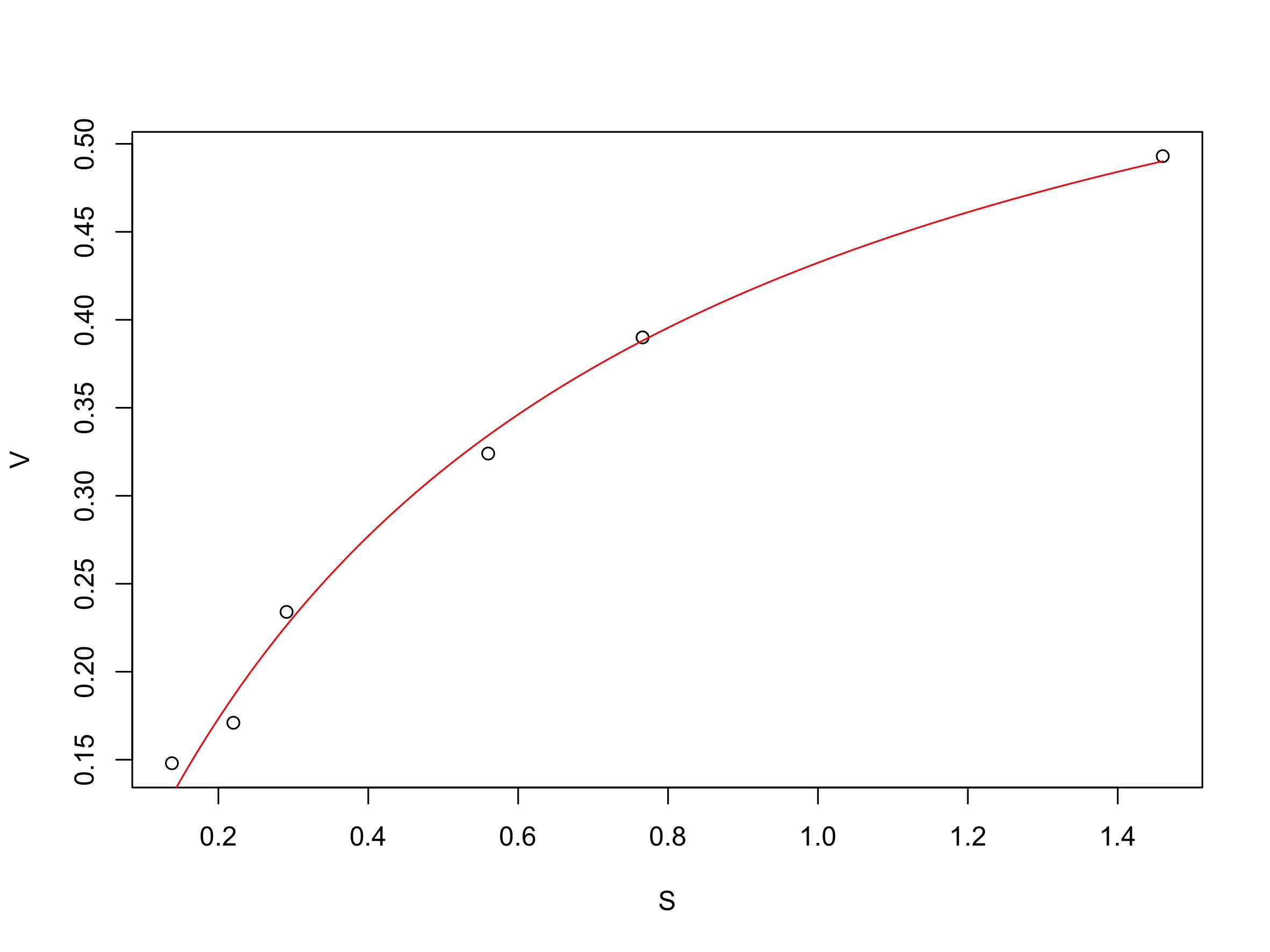
3. Premiers résultats On récupère tout un ensemble de résultats liés à l’ajustement :
Les paramètres estimés : valeurs moyennes (Estimate) et écart-types (Std. Error) ; on obtient la même information avec l’instruction
coef(ajusMM).L’estimation de \(\sigma\) (Residual standard error) ;
La valeur minimum de la \(SCE\) (Residual sum of squares) ;
Vérifiez numériquement la relation entre \(\sigma\) et \(SCE\).
- Et d’autres résultats dont nous ne parlerons pas.
overview(ajusMM)
------
Formula: V ~ vmax * S/(KM + S)
Parameters:
Estimate Std. Error t value Pr(>|t|)
vmax 0.69040 0.03682 18.75 4.77e-05 ***
KM 0.59655 0.06826 8.74 0.000944 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.01356 on 4 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 1.764e-06
------
Residual sum of squares: 0.000736
------
t-based confidence interval:
2.5% 97.5%
vmax 0.5881579 0.7926407
KM 0.4070356 0.7860596
------
Correlation matrix:
vmax KM
vmax 1.0000000 0.9450641
KM 0.9450641 1.00000004. Analyse des résidus - graphiques
residus <- nlsResiduals(ajusMM)
par(mar = c(4, 4, 3, 0.2))
plot(residus)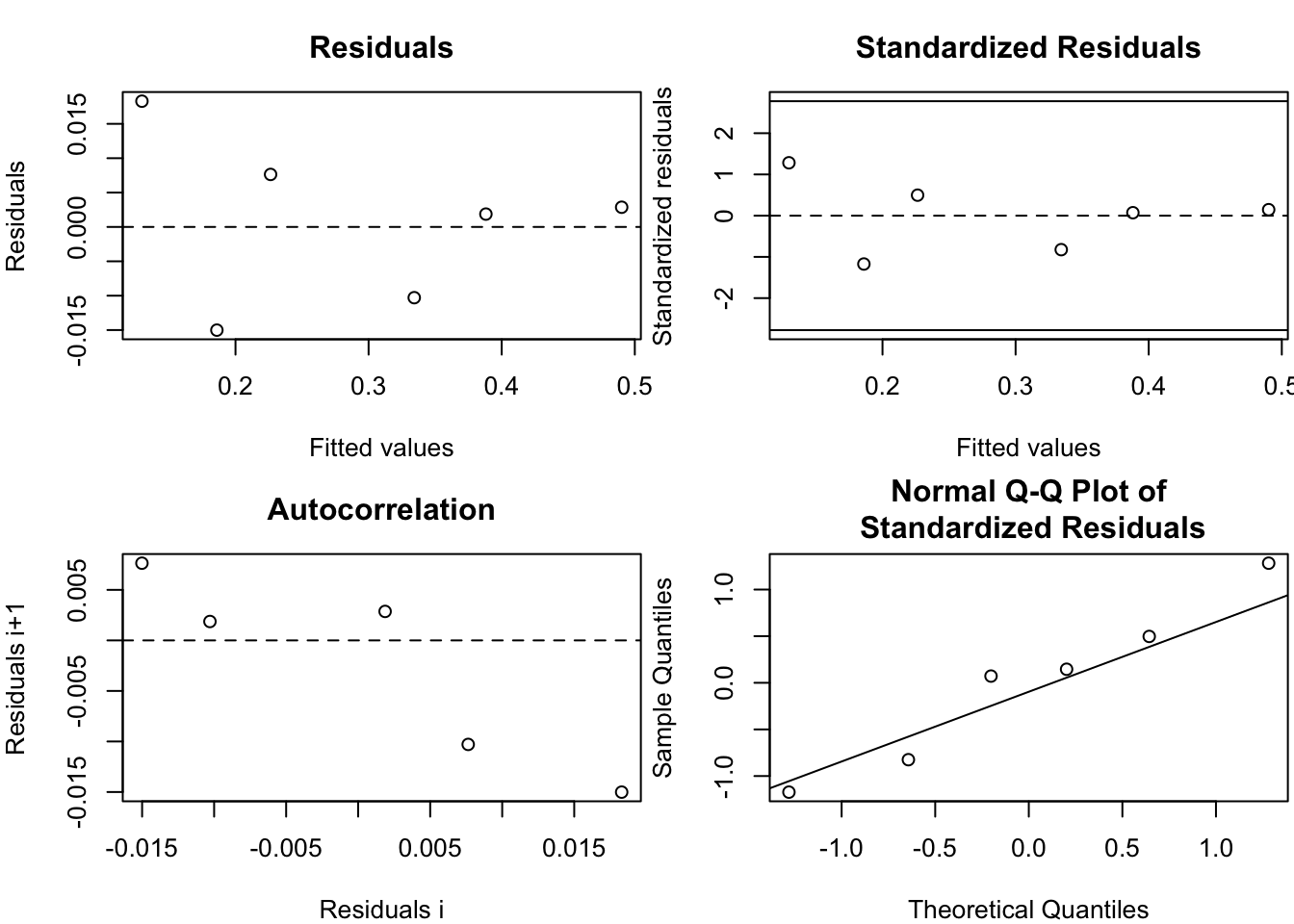
- Qu’en pensez-vous ?
Les résidus standardisés sont les résidus divisés par l’écart-type \(\sigma\). On constate ici une certaine auto-corrélation
4.4.3 Comparaison des deux approches
Nous allons maintenant comparer les valeurs des paramètres estimés par linéarisation de Lineweaver & Burk et par régression non linéaire. Pour faire cette comparaison, nous pouvons par exemple nous appuyer sur l’erreur relative des estimations et sur des graphiques montrant simultanément les deux ajustements.
Nous aurons besoin des objets créés précédemment sous R, en particulier m et ajusMM.
Pour comparer les erreurs relatives, nous devons travailler directement sur les paramètres \(v_{max}\) et \(K_M\).
# Pour la linéarisation
# On a déjà calculé ER.vmax et ER.KM
# Pour la régression non linéaire
estim.nonlin <- summary(ajusMM)$coefficients[,"Estimate"]
SE.nonlin <- summary(ajusMM)$coefficients[,"Std. Error"]
ER.nonlin <- 100*qt(0.975, n-2)*SE.nonlin/estim.nonlin
# Présentation de la comparaison sous forme d'une matrice
comp <- matrix(c(ER.vmax, ER.KM, ER.nonlin), ncol=2, nrow=2)
colnames(comp) <- c("L&B", "MM")
rownames(comp) <- c("vmax", "KM")
print(comp) L&B MM
vmax 49.28430 14.80903
KM 57.09478 31.76813- Que pouvez-vous en conclure ?
Pour les graphiques, on peut choisir soit le plan (\([S]\), \(v\)) du modèle de Michaelis-Menten, soit le plan \((1/[S], 1/v)\) de la linéarisation de Lineweaver & Burk (voir figure ci-dessous).
par(mfrow = c(1,2), mar = c(4,4,2,1))
# Dans le plan ([S], v)
plot(dataMM1$S, dataMM1$V, xlab="[S]", ylab="v", las=1, pch=19, main="Représentation directe", cex.main=0.75, xlim=c(0, max(dataMM1$S)), ylim=c(0, max(dataMM1$V)))
curve(estim.nonlin["vmax"]*x/(estim.nonlin["KM"]+x), from=0, to=max(dataMM1$S), add=TRUE)
curve(vmax*x/(KM+x), from=0, to=max(dataMM1$S), add=TRUE, lty=2)
legend("bottomright", legend=c("MM", "L&B"), lty=c(1,2), bty="n", cex=0.75)
# Dans le plan (1/[S], 1/v)
plot(1/dataMM1$S, 1/dataMM1$V, xlab="1/[S]", ylab="1/v", las=1, pch=19, main="Représentation L&B", cex.main=0.75, xlim=c(0, max(1/dataMM1$S)), ylim=c(0, max(1/dataMM1$V)))
abline(a=1/coef(ajusMM)["vmax"], b=coef(ajusMM)["KM"]/coef(ajusMM)["vmax"])
abline(m, lty=2)
legend("bottomright", legend=c("MM", "L&B"), lty=c(1,2), bty="n", cex=0.75)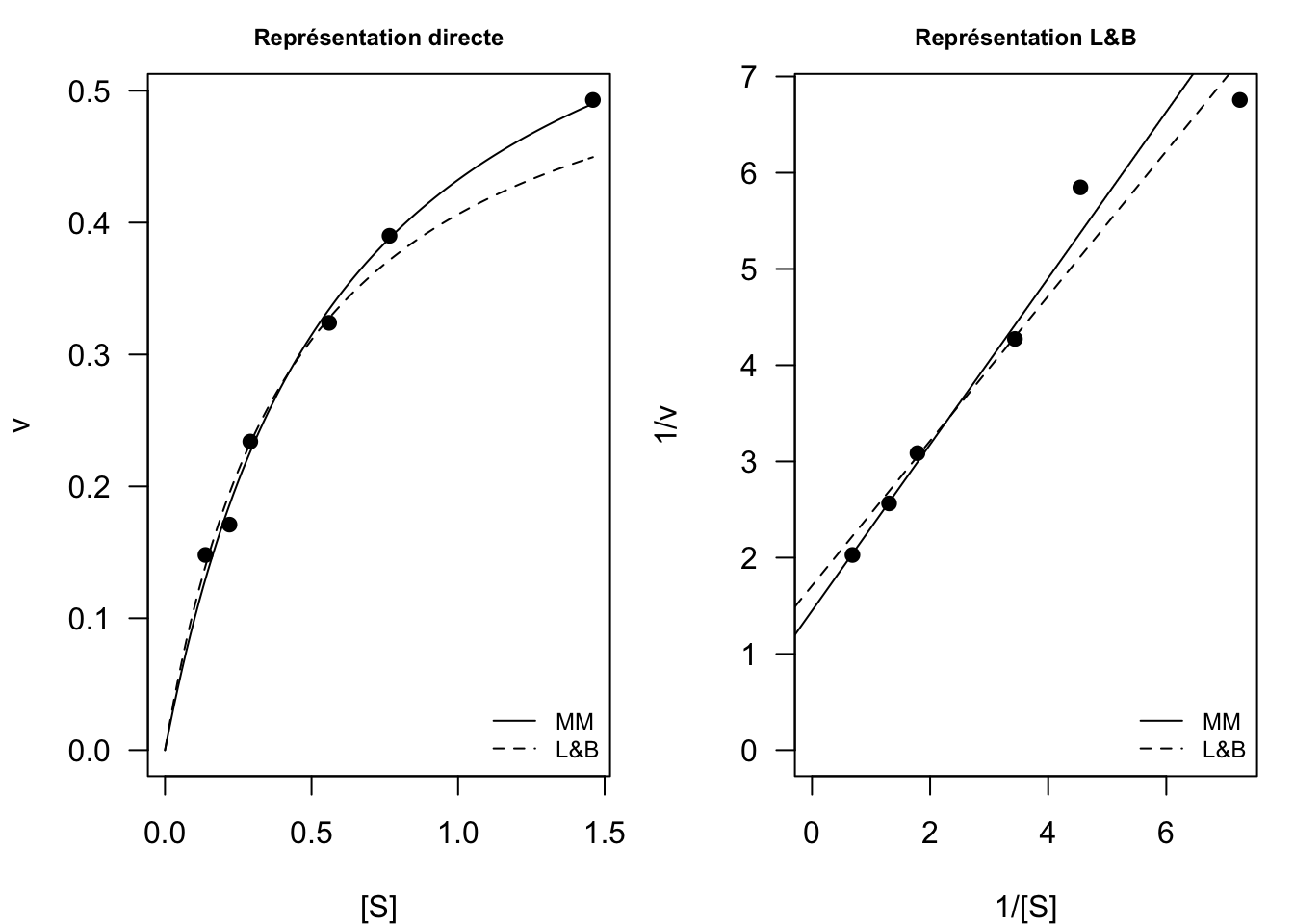
- Que pouvez-vous en conclure ?
On voit sur ces deux graphes que la transformation de L&B donne un plus mauvais ajustement que la régression directe avec le modèle de MM, en particulier pour les fortes valeurs de concentrations en substrat.
4.5 A vous de jouer !
Télécharger les jeux de données 2 et 3.
Pour chaque jeu de données, vous ajusterez les trois transformations linéaires ainsi que la version non linéaire du modèle de Michaelis-Menten.
Pour chaque ajustement :
vous représenterez graphiquement le modèle superposé aux données ;
vous donnerez l’estimation moyenne des paramètres avec l’intervalle de confiance à 95 \(\%\) ;
vous jugerez de la corrélation entre les paramètres ;
vous examinerez les résidus ;
vous vérifierez l’hypothèse de normalité des résidus.
Sur la base de vos résultats, vous discuterez du bien fondé des transformations linéaires.
Vous veillerez également à toujours comparer les résultats de l’ajustement avec le modèle de Michaelis-Menten, aux résultats des ajustements avec les différentes transformations linéaires.